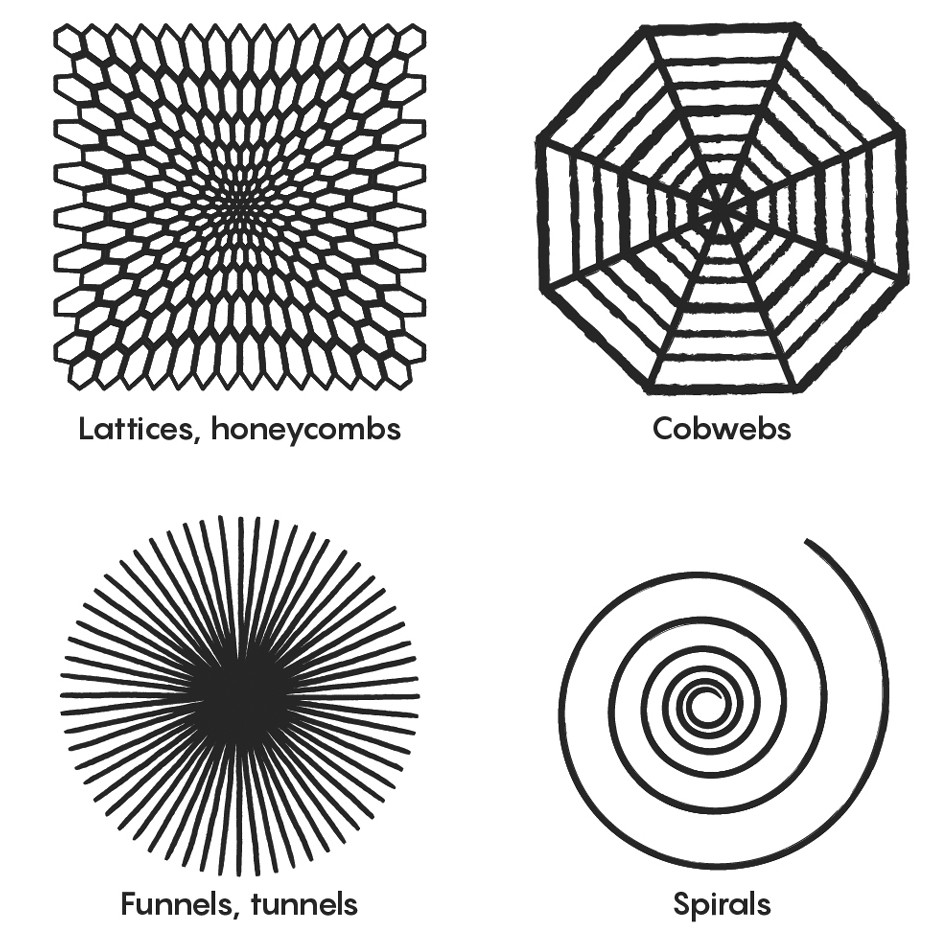
Lattices, funnels, spirals and cobwebs: Why do these patterns reoccur so frequently in nature? And why, when people hallucinate, do they so often report these geometries? Like Alice herself, I inadvertently fell down a rabbit hole following these questions for way too many hours this weekend in a fascinating Quanta article, "A Math Theory for Why People Hallucinate."

The visual cortex is wired in such a way that these patterns, often called "form constants," emerge. "What we see when we hallucinate reflects the architecture of the brain's neural network," article author Jennifer Ouellette wrote. These patterns also occur so much in nature (The tiger's stripes, the bees' honeycomb, the spider's web), something that has been called "Turing Patterns," named after, yes, early computer pioneer, Alan Turing, who developed, in the years following the war, a mathematical formula describing these repeating biological patterns. Why the spatial patterns occur can best be explained through a fanciful analogy to sweating grasshoppers.

Turing’s math described how complex patterns come about in terms of multiple chemicals diffusing themselves through a system at different rates, sometimes interacting with each other to generate patterns. Biologist James Murray illustrated the effect by asking us to consider a dry field filled with grasshoppers. Should you set the field on fire, typically, the entire plot would be left charred. But, what if the fire caused the grasshoppers to sweat, which, in turn, dampened sections of the field wet, and hence, they were left unburned? The pattern in the field then would be a simplified example of a Turing Mechanism.